About Doubling Time Calculator (Formula)
The concept of doubling time is crucial in various fields such as finance, biology, and population studies. Doubling time refers to the period required for a quantity to double in size or value at a constant growth rate. Our Doubling Time Calculator provides an easy and efficient way to determine this time based on the growth rate. Whether you’re analyzing investments, population growth, or any other exponential growth scenario, understanding doubling time is essential.
Formula
The formula for calculating doubling time is as follows:
Doubling Time = (ln(2) / ln(1 + (r/100))) / t
Where:
- ln = natural logarithm
- r = growth rate (as a percentage)
- t = time period
How to Use
- Input the Growth Rate (r): Enter the percentage growth rate of the quantity you’re analyzing.
- Input the Time Period (t): Enter the time period over which the growth occurs (e.g., yearly, monthly).
- Calculate: Press the calculate button to find the doubling time.
- Interpret the Result: The calculator will provide the time required for the quantity to double based on the inputs provided.
Example
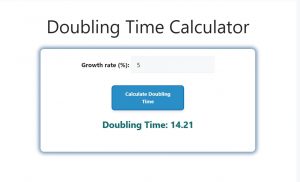
Let’s say you have an investment growing at a rate of 5% per year. To find out how long it will take for the investment to double:
- Growth Rate (r): 5%
- Time Period (t): 1 year
Using the formula:
Doubling Time = (ln(2) / ln(1 + (5/100))) / 1
After calculation, the doubling time will be approximately 14.21 years. This means it will take about 14.21 years for your investment to double in value at a 5% growth rate.
FAQs
1. What is doubling time?
Doubling time is the period it takes for a quantity to double in size or value at a constant growth rate.
2. How is doubling time calculated?
Doubling time is calculated using the formula: Doubling Time = (ln(2) / ln(1 + (r/100))) / t, where r is the growth rate and t is the time period.
3. Why is doubling time important?
Doubling time is crucial for understanding how quickly investments, populations, or other quantities grow over time.
4. Can I use this calculator for any type of growth?
Yes, the calculator can be used for any type of exponential growth, including investments, population growth, and more.
5. What is the natural logarithm (ln)?
The natural logarithm is the logarithm to the base of the number e, where e is approximately 2.71828.
6. What if the growth rate is negative?
If the growth rate is negative, it indicates a decay rather than growth, and the concept of doubling time may not apply in the traditional sense.
7. Does doubling time depend on the initial value?
No, doubling time is independent of the initial value and depends only on the growth rate.
8. What is the relation between growth rate and doubling time?
Higher growth rates result in shorter doubling times, while lower growth rates result in longer doubling times.
9. Can doubling time be used for non-financial purposes?
Yes, doubling time is widely used in fields like biology, environmental science, and demographics, apart from finance.
10. How does the time period (t) affect the calculation?
The time period (t) affects the calculation by indicating the interval at which the growth rate is applied, influencing the doubling time.
11. What is the significance of the ln(2) in the formula?
ln(2) represents the natural logarithm of 2, which is essential for calculating the time it takes for something to double.
12. Can this formula be used for continuous compounding?
Yes, the formula is applicable for continuous compounding situations where growth occurs continuously over time.
13. How accurate is the doubling time calculation?
The accuracy depends on the precision of the input values, but the formula itself is mathematically accurate.
14. Is there a shortcut to estimate doubling time?
A rough estimate can be made using the Rule of 72, where you divide 72 by the growth rate to approximate the doubling time.
15. What is the Rule of 72?
The Rule of 72 is a simplified way to estimate the doubling time by dividing 72 by the annual growth rate percentage.
16. Can I calculate doubling time for varying growth rates?
The provided formula assumes a constant growth rate. For varying rates, a more complex calculation or model is needed.
17. Is there a difference between annual and periodic doubling time?
Yes, periodic doubling time may differ depending on the frequency of compounding (e.g., monthly, quarterly), while annual doubling time is calculated over a year.
18. What happens if the growth rate is extremely high?
An extremely high growth rate will result in a very short doubling time, indicating rapid growth.
19. Can I use this calculator for any currency?
Yes, the calculator works for any currency or unit of measurement as long as the growth rate and time period are consistent.
20. How does inflation affect doubling time?
Inflation can reduce the real growth rate, thereby increasing the actual time it takes for an investment or quantity to double in value.
Conclusion
Understanding doubling time is vital for making informed decisions in various fields, from finance to biology. Our Doubling Time Calculator simplifies this process, allowing you to quickly determine how long it will take for your investments or other quantities to double in value. By knowing the doubling time, you can better plan and manage growth expectations, ensuring more accurate and effective strategies.
